In the realm of physics and everyday life, the concepts of speed and velocity are often used interchangeably, but they have distinct meanings and implications. Understanding the difference between speed and velocity is essential for comprehending various physical phenomena accurately. While both terms deal with the rate of motion, they differ in terms of direction and how they are measured. In this article, we will delve into the details of speed and velocity, exploring their definitions, characteristics, equations, and practical applications. By the end, you will have a clear understanding of the disparities between these two fundamental concepts.
Table of Contents
Key Differences Between Speed and Velocity: Table
Before going into details, here’s a comparison table illustrating the key differences between speed and velocity:
| Aspect | Speed | Velocity |
|---|---|---|
| Definition | Speed refers to the rate at which an object covers a certain distance. It measures how quickly an object moves, without considering its direction. | Velocity refers to the rate at which an object changes its position in a certain direction. It combines speed with direction, providing information on how fast an object is moving and in which direction. |
| Type of quantity | Speed is a scalar quantity, as it only has magnitude and no specific direction associated with it. | Velocity is a vector quantity since it has both magnitude and direction. |
| Magnitude | Speed can never be negative or zero. It is always a positive value. | Velocity can be zero, negative, or positive, depending on the direction of motion. A positive velocity indicates motion in one direction, while a negative velocity indicates motion in the opposite direction. |
| Change of direction | Speed does not consider the change in direction. It only focuses on the overall distance covered. | Velocity takes into account the change in direction. If an object changes its direction, its velocity changes accordingly. |
| Interrelation | Speed may or may not be equal to velocity. Two objects can have the same speed but different velocities if they are moving in different directions. | An object may possess different velocities but the same speed. This can happen if the object changes direction but maintains the same average speed over a certain period. |
| Unit (SI) | Both speed and velocity are measured in meters per second (m/s) in the SI system. | Both speed and velocity are quantified using the same unit, meters per second (m/s), in the International System of Units (SI). |
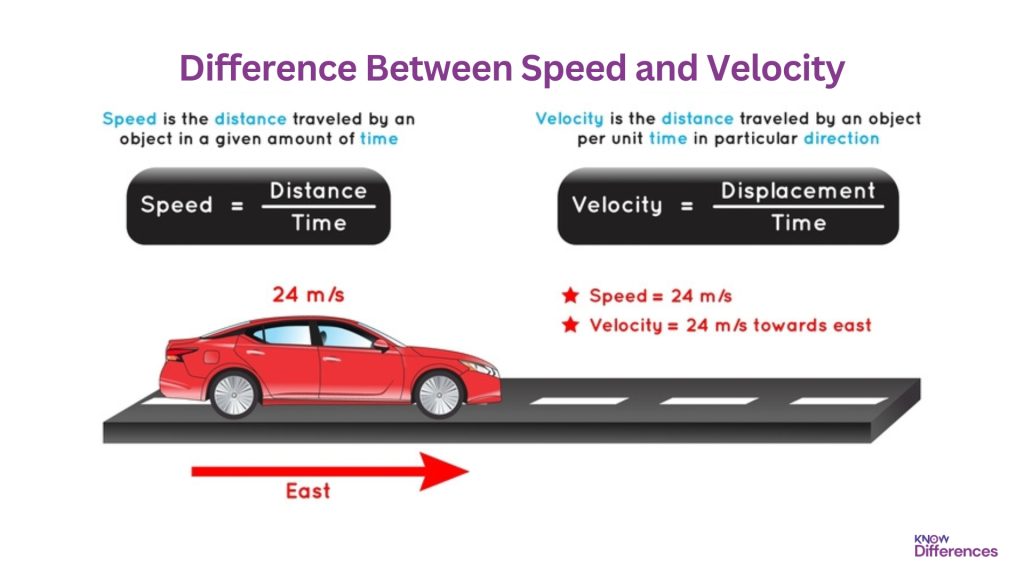
| Equation | Speed (v) is calculated by dividing the distance (d) traveled by the time (t) taken: v = d/t. | Velocity (v) is determined by dividing the displacement (∆x) by the time (∆t) it takes to cover that displacement: v = ∆x/∆t. Displacement refers to the change in position of the object, considering direction. |
| Example | Imagine a car driving along a straight road at a constant speed of 60 km/h. Here, the car’s speed is 60 km/h, but since the road is straight and the car is not changing direction, its velocity is also 60 km/h in the direction it is moving. | Consider a person running around a circular track. If the person completes one lap and returns to the starting point in 1 minute, the average speed will be calculated based on the total distance covered divided by the time taken. However, since the person ends up at the starting point and doesn’t change their overall position, their velocity will be zero, even though the speed is not zero. |
Overview of Speed
Definition of Speed
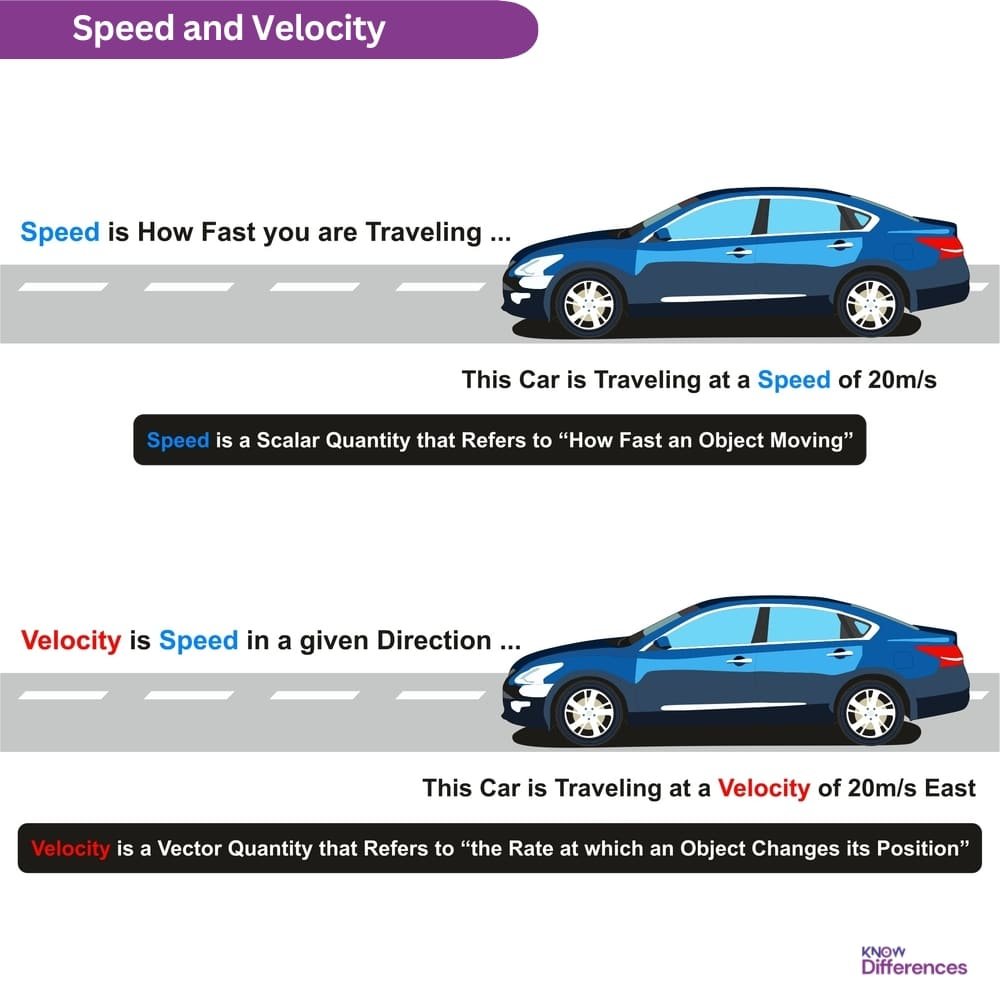
Speed can be defined as the rate at which an object covers a certain distance. It focuses on how quickly an object moves without considering the direction of motion. Speed is a fundamental concept used to measure how fast an object travels, providing information solely about the magnitude of the motion.
Speed as a Scalar Quantity
Speed is a scalar quantity. This means that it has magnitude but does not possess a specific direction associated with it. Scalar quantities, such as speed, are represented by single numerical values.
Magnitude of Speed
Speed can never be negative or zero. It is always a positive value, representing the absolute value of the rate of motion. For instance, if a car is traveling at a speed of 60 kilometers per hour, it means that the car is covering a distance of 60 kilometers every hour.
Types of Speed
- Instantaneous Speed: This refers to the speed of an object at a particular instant in time. It is calculated by determining the distance covered in an infinitesimally small time interval.
- Average Speed: Average speed is calculated by dividing the total distance traveled by an object by the total time taken. It provides an overall measure of the object’s speed over a given period.
- Tangential Speed: Tangential speed refers to the speed of an object moving along a circular path. It represents the rate at which an object covers the arc length of the circle per unit time.
- Rotational Speed: Rotational speed, also known as angular speed, is applicable to objects that rotate around an axis. It represents the rate at which an object completes a full rotation or revolution in a given time.
Uniform and Non-Uniform Speed
Uniform speed and non-uniform speed are not types of speed. Instead, they describe the characteristics of an object’s motion in relation to its speed.
Uniform Speed
Uniform speed refers to the motion of an object at a constant rate, where the object covers equal distances in equal intervals of time. In other words, the speed remains the same throughout the entire motion, without any changes in magnitude or direction. An object moving at uniform speed follows a straight line path and maintains a constant velocity, indicating a consistent rate of displacement per unit of time.
Some key characteristics of uniform speed include:
- Constant Magnitude: The magnitude of the speed remains unchanged throughout the motion. For example, if a car travels at a uniform speed of 60 kilometers per hour, it maintains this speed without any fluctuations.
- Equal Intervals: The object covers equal distances in equal intervals of time. For instance, if a car travels 60 kilometers in 1 hour at a uniform speed, it will cover 30 kilometers in half an hour.
- Straight-Line Path: The object moves along a straight-line path without deviating or changing direction. This means that the object does not experience any acceleration or deceleration during its motion.
Examples of uniform speed in daily life include a car traveling on a highway at a constant speed, a person walking at a consistent pace, or a satellite orbiting the Earth at a stable velocity.
Non-Uniform Speed
Non-uniform speed refers to the motion of an object where the speed changes at different points during its journey. Unlike uniform speed, the object does not cover equal distances in equal intervals of time. Non-uniform speed can result from various factors, such as changes in acceleration, uneven terrain, or external forces acting on the object.
Key characteristics of non-uniform speed include:
- Varying Magnitude: The speed of the object changes at different stages of its motion. It can increase, decrease, or fluctuate irregularly, indicating a changing rate of displacement per unit of time.
- Unequal Intervals: The object covers unequal distances in equal intervals of time or equal distances in unequal intervals of time. This means that the object’s speed is not constant throughout its journey.
- Curved Path: The object may follow a curved or non-linear path, experiencing changes in direction or acceleration. It may accelerate or decelerate at different points, leading to variations in speed.
Examples of non-uniform speed include a car accelerating from rest and then slowing down at a traffic signal, a person running at different speeds during a marathon race, or a roller coaster moving at varying speeds throughout its track.
Understanding the distinction between uniform and non-uniform speed allows us to analyze and describe the motion of objects in different situations, accounting for changes in speed, time intervals, and path curvature.
Examples and Applications of Speed
Speed plays a crucial role in various real-life scenarios and scientific applications. In sports, speed determines the performance of athletes, such as sprinters or racing drivers. It is also essential in transportation, as the speed of vehicles affects travel times and efficiency. Moreover, understanding speed is vital in fields like engineering, physics, and meteorology, where accurate measurements of motion are necessary for calculations, experiments, and weather forecasting.
Overview of Velocity
Definition of Velocity
Velocity, on the other hand, goes beyond the concept of speed by incorporating the element of direction. It refers to the rate at which an object changes its position in a specific direction. Velocity provides a comprehensive description of an object’s motion, taking into account both the magnitude and direction of movement.
Velocity as a Vector Quantity
Unlike speed, which is a scalar quantity, velocity is a vector quantity. This means that it possesses both magnitude and direction and requires specific mathematical representation to fully describe the motion.
Magnitude and Direction of Velocity
Velocity can be zero, negative, or positive, depending on the direction of motion. A positive velocity indicates motion in one direction, while a negative velocity indicates motion in the opposite direction. The magnitude of velocity represents the speed component, while the direction indicates the path or trajectory of the object’s motion.
Types of Velocity
- Instantaneous Velocity: Similar to instantaneous speed, instantaneous velocity refers to the velocity of an object at a specific instant in time. It takes into account both the magnitude and direction of the object’s motion.
- Average Velocity: Average velocity is calculated by dividing the displacement of an object by the time taken. Displacement refers to the change in position of the object, considering both magnitude and direction.
- Uniform Velocity: Uniform velocity occurs when an object travels at a constant speed in a straight line without any change in direction. In this case, the magnitude and direction of velocity remain constant.
- Variable Velocity: Variable velocity describes the motion of an object when its speed or direction changes. The magnitude and/or direction of velocity vary throughout the object’s motion.
- Relative Velocity: Relative velocity refers to the velocity of an object as observed from another moving object. It takes into account the motion of both objects and considers their relative positions and velocities.
- Terminal Velocity: Terminal velocity is the constant velocity achieved by an object falling through a fluid, such as air or water. At terminal velocity, the object experiences a balance between the gravitational force pulling it downwards and the drag force exerted by the fluid.
Examples and Applications of Velocity
Velocity is a fundamental concept in various fields, including physics, engineering, and navigation. In physics, velocity is crucial for analyzing the motion of objects, predicting trajectories, and understanding complex systems. In engineering, velocity is utilized to calculate the forces acting on structures or fluid dynamics. In navigation, velocity plays a vital role in determining the speed and direction of vehicles, such as ships or aircraft.
Comparing Speed and Velocity
Change in Direction
One of the key distinctions between speed and velocity lies in their treatment of direction changes. Speed does not consider changes in direction; it only focuses on the overall distance covered. On the other hand, velocity takes into account the change in direction. If an object changes its direction while moving, its velocity changes accordingly, reflecting the alteration in both magnitude and direction.
Interrelation between Speed and Velocity
While speed and velocity are related, they are not interchangeable. An object may possess different velocities but the same speed. This occurs when an object changes direction but maintains the same average speed over a certain period. Conversely, two objects can have the same speed but different velocities if they are moving in different directions.
The formula for Speed and Velocity
Speed is calculated by dividing the distance traveled (d) by the time taken (t):
v = d/t
Velocity, on the other hand, is determined by dividing the displacement (∆x) by the time (∆t) it takes to cover that displacement:
v = ∆x/∆t.
Displacement refers to the change in position of the object, considering both magnitude and direction.
Examples Highlighting the Differences
To illustrate the disparities between speed and velocity, let’s consider a few examples. Imagine a car driving along a straight road at a constant speed of 60 kilometers per hour. In this case, the car’s speed is 60 km/h, and since the road is straight and the car is not changing direction, its velocity is also 60 km/h in the direction it is moving.
Now, suppose a person is running around a circular track. If the person completes one lap and returns to the starting point in 1 minute, the average speed will be calculated based on the total distance covered divided by the time taken. However, since the person ends up at the starting point and doesn’t change their overall position, their velocity will be zero, even though the speed is not zero.
Conclusion
In conclusion, understanding the difference between speed and velocity is essential for accurately describing and analyzing various physical phenomena. While speed measures the rate at which an object covers a distance, velocity incorporates both magnitude and direction, providing a comprehensive picture of motion. By grasping these concepts and their distinctions, we can delve deeper into the world of physics, engineering, and everyday experiences, enabling us to make more informed observations and calculations. So, the next time you discuss the motion of objects, remember the disparities between speed and velocity and appreciate their unique roles in our understanding of the physical universe.
FAQs: Speed vs. Velocity
What are the main differences between speed and velocity?
Speed refers to the rate at which an object covers a certain distance, without considering direction. Velocity includes both the magnitude and direction of motion. While speed is a scalar quantity, velocity is a vector quantity.
When are speed and velocity the same?
Speed and velocity are the same when an object moves in a straight line without changing direction. In such cases, the magnitude of the velocity (speed) and the direction of motion coincide, resulting in equal speed and velocity.
Is velocity always equal to speed?
No, velocity is not always equal to speed. Velocity takes into account both the magnitude and direction of motion, whereas speed only considers the magnitude. If an object changes its direction while moving, its velocity changes, even if the speed remains the same.
In which situation does the magnitude of speed and velocity become equal?
The magnitude of speed and velocity becomes equal when an object moves in a straight line without any change in direction. In this scenario, the object’s speed (magnitude of velocity) and the direction of motion align perfectly, resulting in equal magnitude for both speed and velocity.
Are speed and velocity the same in a straight line?
Yes, speed and velocity are the same in a straight line when an object moves without changing its direction. In this case, the magnitude of the velocity (speed) remains constant, and the direction of motion is consistent, resulting in equal speed and velocity