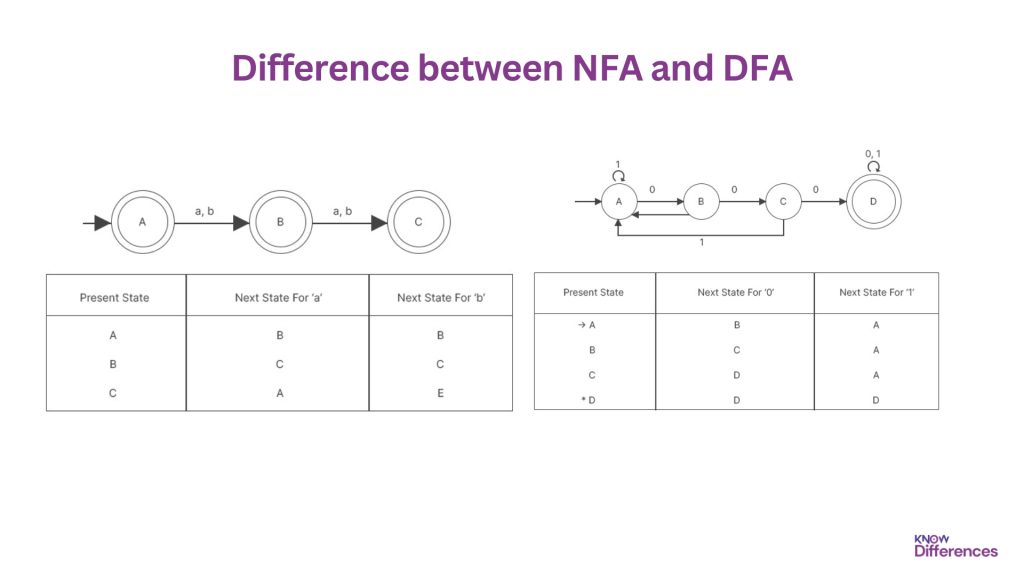
Nondeterministic Finite Automata (NFA) and Deterministic Finite Automata (DFA) are fundamental concepts in automata theory and play a crucial role in computer science and theoretical computer science. Understanding the differences between NFA and DFA is essential for grasping the underlying principles of these models and their applications.
In this comprehensive article, we will explore the difference between NFA and DFA, covering various aspects in detail. From state transitions to execution time, we will delve into each characteristic, providing clear explanations and examples along the way. By the end of this article, you will have a solid understanding of the disparities between NFA and DFA, their strengths, and their limitations.
Table of Contents
What is an Automaton?
Before diving into the differences between NFA and DFA, let’s start by understanding the concept of an automaton. In computer science, an automaton refers to an abstract mathematical model that represents a computing device or machine. Automata are employed to study and analyze the capabilities and behavior of such machines in processing languages or recognizing patterns.
What is a Finite Automaton?
A finite automaton is a specific type of automaton that operates on a finite sequence of inputs. It consists of a finite set of states, an alphabet of input symbols, a transition function that describes the movement between states based on the input, and a set of accepting states that determine whether a particular input sequence is accepted or rejected by the automaton.
Let’s begin by understanding the fundamental definitions of NFA and DFA.
A Deterministic Finite Automaton (DFA) is a mathematical model consisting of a set of states, an input alphabet, a transition function, an initial state, and a set of accepting states.
On the other hand, a Nondeterministic Finite Automaton (NFA) follows a similar structure but allows for more flexibility in state transitions.
DFA vs NFA: Comparison Table
Here is the table comparing the differences between DFA and NFA:
| Aspect | DFA | NFA |
|---|---|---|
| Definition | Deterministic Finite Automata (DFA) | Nondeterministic Finite Automata (NFA) |
| State Transitions | One state transition for each symbol | Multiple possible next states for each symbol |
| Empty String Transition | Not allowed | Can use Empty String transition |
| Comprehension | One machine | Multiple little machines computing concurrently |
| Next State Determinism | Next state is distinctly set | Multiple possible next states for each pair of state and input symbol |
| Construction Difficulty | More difficult | Easier to construct |
| String Rejection | Terminates in a non-accepting state | All branches die or refuse the string |
| Execution Time | Less time needed for executing an input string | More time needed for executing an input string |
| Relationship | All DFA are NFA | Not all NFA are DFA |
| Space Requirement | Requires more space | Requires less space than DFA |
| Dead Configuration | Not allowed | Allowed |
| Transition Function | δ: Q x Σ → Q | δ: Q x Σ → 2Q |
| Backtracking | Allowed | Not always possible |
| Regular Expression Conversion | Difficult | Simpler compared to DFA conversion |
| Epsilon Move | Not allowed | Allowed |
| Moves for Single Input Alphabet | Only one move | Choice of more than one move |
Understanding Deterministic Finite Automaton (DFA)
A Deterministic Finite Automaton (DFA) is an automaton that exhibits determinism, meaning that for every state and input symbol, there is precisely one unique next state. Unlike NFAs, DFAs do not possess the ability to be in multiple states simultaneously while processing an input symbol. DFAs follow a precisely defined set of rules, making their behavior predictable.
DFA: A Deterministic Finite Automaton (DFA) is a mathematical model consisting of five components. These components are represented as a five-tuple:
M = (Q, Σ, δ, q0, F)
Here’s what each component represents:
- Q: A finite set of states that the automaton can be in.
- Σ: A finite set of symbols, known as the alphabet, which represents the input the automaton can receive.
- δ: The transition function that maps a current state and an input symbol to a new state. This function is deterministic, meaning it produces a unique state for each combination of state and symbol.
- q0: The initial state from which the automaton starts.
- F: The set of final or accept states, indicating the successful completion of a computation or recognition process.
DFA Transition Function
In a DFA, the transition function maps the current state and an input symbol to a unique next state. This deterministic nature of the transition function enables a DFA to determine its exact next state based on the current state and the input symbol being processed.
DFA Acceptance
For a string to be accepted by a DFA, it must lead to an accepting state when processed from the initial state. The acceptance criteria of a DFA are deterministic, as there is only one unique computation path leading to acceptance.
Understanding Nondeterministic Finite Automaton (NFA)
A Nondeterministic Finite Automaton (NFA) is an automaton that possesses the ability to be in multiple states simultaneously while processing an input symbol. This non-uniqueness of the next state distinguishes NFAs from their deterministic counterparts. NFAs exhibit a degree of flexibility and non-determinism, allowing them to explore multiple paths simultaneously during the computation.
A Nondeterministic Finite Automaton (NFA) shares similarities with a DFA but has a different transition function. It is also represented by a five-tuple:
M = (Q, Σ, δ, q0, F)
Here’s how each component is defined in an NFA:
- Q: A finite set of states that the automaton can be in.
- Σ: A finite set of input symbols, representing the alphabet.
- δ: The transition function, which maps a current state and an input symbol to a set of states. Unlike in a DFA, this function can produce multiple possible states for a given combination of state and symbol.
- q0: The initial state from which the automaton begins its operation.
- F: The final state or states that indicate successful completion of a computation or recognition process.
NFA Transition Function
In an NFA, the transition function maps the current state, an input symbol, and all possible next states. Unlike a DFA, where a unique transition exists for each combination of state and input symbol, an NFA’s transition function may yield multiple potential next states for a given input symbol and current state.
NFA Acceptance
For an input sequence to be accepted by an NFA, at least one possible computation path must lead to an accepting state. The acceptance criteria of an NFA are non-deterministic in nature, as there can be several different paths leading to acceptance.
Key Differences between NFA and DFA
State Transitions
In a DFA, there is precisely one state transition for each symbol in the input alphabet. This deterministic behavior ensures that, given a current state and an input symbol, the next state is uniquely determined. In contrast, an NFA allows for multiple possible next states for each symbol. This non-deterministic characteristic opens up the possibility of parallel computations and diverse paths.
Empty String Transition
One key distinction between NFA and DFA lies in their treatment of empty string transitions. DFA does not allow transitions based on an empty string, whereas NFA permits the use of empty string transitions. An empty string, denoted as ε, represents a transition without consuming any input symbol. This feature gives NFAs an advantage in terms of expressive power and flexibility.
Comprehension
Conceptually, a DFA represents a single machine that processes input strings. In contrast, an NFA can be thought of as multiple little machines computing concurrently. These parallel computations in an NFA enable more flexible state exploration and potentially enhance computational efficiency.
Next State Determinism
DFA exhibits next state determinism, meaning that for a given pair of state and input symbols, the next state is distinctly set. In contrast, NFA allows for multiple possible next states for each pair of state and input symbol. This non-deterministic nature of NFA provides more options but also increases the complexity of determining the next state.
Construction Difficulty
When it comes to constructing automata, DFA construction is generally more challenging compared to NFA construction. The deterministic nature of DFA requires careful consideration of all possible state transitions for each input symbol, leading to a more intricate design process. In contrast, NFA construction can be relatively easier due to the flexibility and parallelism it offers.
String Rejection
In terms of string rejection, DFA and NFA differ in their behaviors. When a DFA encounters a string that is not accepted, it terminates in a non-accepting state. In contrast, an NFA rejects a string if all branches or paths end in non-accepting states or if no path can be taken for a particular input symbol. This distinction highlights the divergent ways in which DFA and NFA handle rejected strings.
Execution Time
The execution time for processing an input string differs between DFA and NFA. Generally, DFA requires less time to execute an input string due to its deterministic nature. With only one possible state transition for each symbol, DFA follows a predictable path throughout the computation. In contrast, NFA may require more time for execution as it explores multiple paths concurrently, potentially leading to increased computational overhead.
Relationship
In terms of their relationship, it is important to note that all DFAs are, in fact, NFAs. This relationship arises from the fact that the deterministic behavior of a DFA can be viewed as a special case of the nondeterministic behavior of an NFA. However, it is crucial to remember that not all NFAs can be represented as DFAs, as the nondeterministic aspects of NFAs often exceed the expressive power of DFAs.
Space Requirement
The space requirement is another aspect where DFA and NFA exhibit differences. Due to the deterministic nature and the need to track a unique state, DFAs generally require more space compared to NFAs. On the other hand, NFAs can utilize more compact representations, benefiting from the flexibility and parallelism in their state transitions.
Dead Configuration
While DFA does not allow dead configurations, which are configurations where no further transitions are possible, NFAs permit them. Dead configurations can occur in NFAs when all possible paths or branches for a particular input symbol lead to non-accepting states or when no path can be taken at all. This characteristic further highlights the differences in behavior between DFA and NFA.
Transition Function
The transition function is a fundamental component of both DFA and NFA.
In a DFA, the transition function is represented as:
δ: Q x Σ → Q
where,
Q represents the set of states and Σ represents the input alphabet.
This function uniquely determines the next state based on the current state and the input symbol.
In an NFA, however, the transition function is represented as:
δ: Q x Σ → 2Q
where,
2Q denotes the power set of Q.
This representation allows for multiple possible next states for each state and input symbol combinations.
Backtracking
Backtracking refers to the ability of an automaton to revisit and explore alternative paths during the computation. While DFA allows backtracking, NFA does not always permit it. The non-deterministic nature of NFA, with its multiple possible next states, creates a more parallel and exploratory approach that doesn’t necessarily involve revisiting previously traversed paths.
Regular Expression Conversion
Converting automata into regular expressions is an essential process in automata theory. When it comes to conversion, DFA poses a greater challenge compared to NFA. Transforming a DFA into a regular expression requires more intricate algorithms and techniques. Conversely, converting an NFA to a regular expression is relatively simpler, benefiting from the inherent flexibility and parallelism of NFAs.
Epsilon Move
The inclusion of epsilon moves is another contrasting feature between DFA and NFA. DFA does not allow transitions based on an empty string (ε). In contrast, NFA permits the use of epsilon moves, where an empty string transition can occur. Epsilon moves provide additional flexibility and can enhance the expressive power of an NFA by enabling transitions without consuming any input symbol.
Moves for Single Input Alphabet
In DFA, a single move is allowed for each input symbol in the input alphabet. The deterministic nature of DFA ensures that the machine follows a unique path for every symbol encountered. On the other hand, NFA allows for the choice of more than one move for a single input alphabet. This non-determinism allows for parallel exploration and the possibility of multiple paths for a given input symbol.
Conclusion
In conclusion, understanding the differences between NFA and DFA is crucial for grasping the principles of automata theory and its applications. The dissimilarities in state transitions, empty string transitions, comprehension, next state determinism, construction difficulty, string rejection, execution time, relationship, space requirement, dead configuration, transition function, backtracking, regular expression conversion, epsilon moves, and moves for single input alphabet highlight the unique characteristics of both models.
While DFA provides determinism and simplicity at the cost of expressive power, NFA introduces non-determinism and flexibility, enabling parallel computations and enhanced expressiveness. Each model has its strengths and limitations, making them suitable for different problem domains and computational requirements.
By thoroughly understanding the differences between NFA and DFA, researchers, computer scientists, and enthusiasts can apply these concepts effectively, design efficient algorithms, and explore the vast realm of formal languages and automata theory.